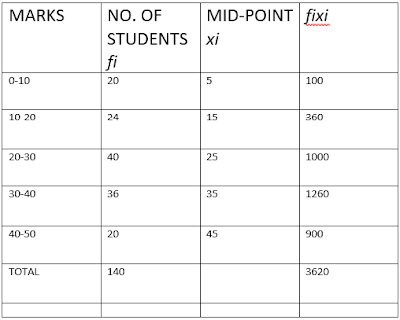
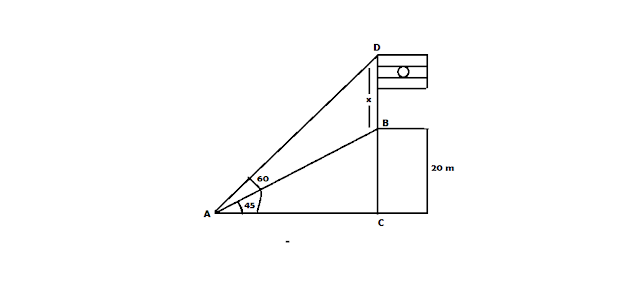
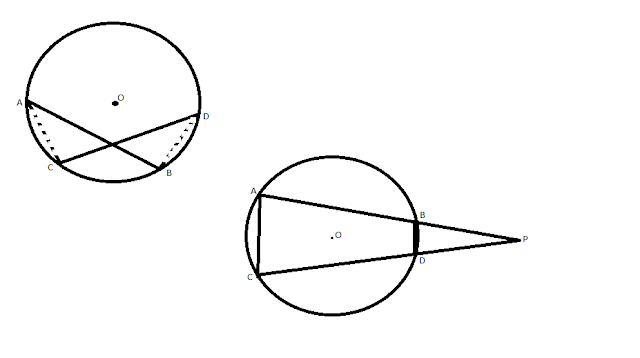
MISCELLANEOUS QUESTIONS
THERE IS 40% INCREASE IN AN AMOUNT IN 8 YEARS AT SIMPLE INTEREST. WHAT WILL BE THE COMPOUND INTEREST IN RS OF RS 30000 AFTER 2 YEARS AT THE SAME RATE? ACCORDING TO THE QUESTION, IF THE PRINCIPLE = RS 100 THEN INTEREST = RS 40 THEREFORE RATE = ( I * 100 ) / ( P * T ) = 40 * 100 * 1/100 * 1/8 = 5 % p. a. CASE II, A = P[1+R/100]^T A = 30000[1+5/100]^2 A = 30000[1+1/20]^2 A = 30000 * 21/20 * 21/20 A = RS 33075 THEREFORE, = RS [33075 - 30000] = RS 3075 WHAT IS THE MEASURE OF THE CENTRAL ANGLE OF THE ARC WHOSE LENGTH IS 11 CM AND RADIUS OF THE CIRCLE IS 14 CM? ARC LENGTH IS 11 CM AND IF WE CALCULATE THE CIRCUMFERENCE OF THE CIRCLE, = 2 * pi * r = 2 * 22/7 * 14 = 88 cm AND NOW WE HAVE TO FIND THE ANGLE OF THE ARC, WE KNOW THAT IN A CIRCLE THE ANGLE IN THE MIDDLE IS 360 deg SO, 88cm = 360 deg 1 cm = 360 / 88 AND IN ARC WHICH IS 11 cm, 11 cm = 360/88 * 11 = 45 deg IF THE SHOPKEEPER SELLS AN ITEM AT RS 960 WHICH IS MARKED AS RS 1200...