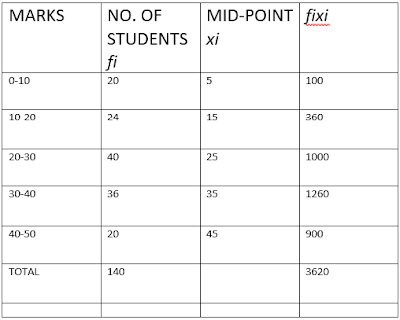
HEIGHT AND DISTANCE

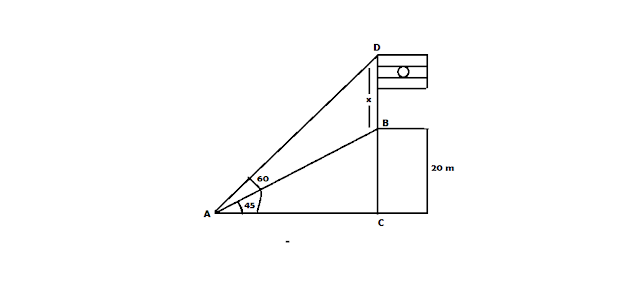
FROM A POINT A ON THE GROUND, THE ANGLE OF ELEVATION OF THE TOP OF A 20 m TALL BUILDING IS 45. A FLAG IS HOSTED AT THE TOP OF THE BUILDING AND THE ANGLE OF ELEVATION OF THE TOP OF THE FLAGSTAFF FROM A IS 60. FIND THE LENGTH OF THE FLAGSTAFF AND THE DISTANCE OF THE BUILDING FROM THE POINT A.

LET "BC" BE THE BUILDING AND "BD" BE A FLAG

GIVEN,       BC=20 m   ANGLE(BAC)=45     ANGLE(DAC)= 60

LET      BD= x m

IN TRIANGLE(BAC),       tan45 = BC/AC = 20/AC

AC = 20 m

NOW IN TRIANGLE(DCA),     DC = DB + BC = x + 20

tan 60 = DC/AC

sqrt(3) = (x + 20)/20

x + 20 = 20*sqrt(3) = 20 * 1.732 = 34.64

x = 34.64 - 20 = 14.64 m

HENCE, THE LENGTH OF THE FLAGSTAFF IS 14.64 M AND DISTANCE OF POINT A FROM THE BUILDING IS 20 m.

TWO POLES ARE PLACED AT P AND Q ON EITHER SIDE OF A ROAD SUCH THAT THE LINE JOINING P AND Q IS PERPENDICULAR TO THE LENGTH OF THE ROAD. A PERSON MOVES x METRE AWAY FROM P PARALLEL TO THE ROAD AND PLACES ANOTHER POLE AT R. THEN THE PERSON MOVES FURTHER x METRE IN THE SAME DIRECTION AND TURNS AND MOVES A DISTANCE Y METRES AWAY FROM THE ROAD PERPENDICULARLY, WHERE HE FINDS HIMSELF Q AND R ON THE SAME LINE. THE DISTANCE BETWEEN P AND Q (i,e., THE WIDTH OF THE ROAD) IN METRE IS

THIS QUESTION IS LENGTHY BUT IF READ IT CAREFULLY IT IS VERY EASY AND AS WELL AS SOLUTION IS ALSO VERY EASY.

THIS QUESTION CAN BE ASKED IN ANY COMPETITION EXAMS AND BY SEEING THIS QUESTION MANY STUDENTS LEAVE IT BUT IT IS JUST 20 TO 30 SECONDS QUESTION

IN TRIANGLE PQR AND TRIANGLE RST

angle TRS = angle PRQ

angle TSR = angle RPQ = 90 degree

BY AA THEY ARE SIMILAR

TRIANGLE PQR IS CONGUENT TO TRIANGLE RST

THEREFORE RS/ST = PR/PQ

x/y = x/PQ

PQ = y metre