SSC TRICKS FOR MATHS

CUBE d = side VOLUME : V = d^2 SURFACE AREA : S = 6(d^2) RECTANGULAR SOLID l = length, w = width, h = height VOLUME: V = lwh SURFACE AREA : S = 2lw + 2lh + 2wh SPHERE r = radius VOLUME : V = 4/3*pi*r^3 SURFACE AREA : S = 4*pi*r^2 RIGHT CIRCULAR CYLINDER r = radius, h = height VOLUME : V = pi*r^2*h SURFACE AREA : S = 2*pi*r*h + 2 *pi*r^2 TORUS r = tube radius, R = torus radius VOLUME : V = 2*pi^2*r^2*R SURFACE AREA : S = 4*pi^2*r*R PYRAMID A = area of base , h = height VOLUME : V = 1/3*A*h RIGHT CIRCULAR CONE r = radius, h = height VOLUME : V = 1/3*pi*r^2*h SURFACE AREA : S = pi*r*[sqrt(r^2 + h^2)] + pi*r^2 FRUSTUM OF A CONE r = radius, R = base radius, h = height, s = slant height VOLUME : V = pi/3(r^2 + rR + R^2)h SURFACE AREA : S = pi*s(R+r) + pi*r^2 + pi*R^2 SQUARE PYRAMID s = side, h = height VOLUME : V = 1/3*s^2*h SURFACE AREA :

CIRCLE r = radius; d = diameter DIAMETER : d = 2r AREA : A = (pi) r^2 CIRCUMFERENCE : C = 2(pi)r = (pi)d SECTOR r = radius; angle(AOB) = angle in radius AREA : A = 1/2 (pi) r^2 ARC LENGTH : s = angle(AOB) r ELLIPSE a = semimajor axis b = semiminor axis AREA : A = (pi) ab CIRCUMFERENCE : C = (pi)[3(a+b) - sqrt{(a+3b)(b+3a)} ANNULUS  (COCENTRIC CIRCLES) r = inner radius, R = outer radius AVERAGE RADIUS = 1/2(r+R) WIDTH : w = R-r AREA : A = pi(R^2 - r^2) or A = 2*pi*22/7*average radius*width REGULAR POLYGON s = side length, n = number of sides CIRCUMFERENCE : R = 1/2*s*cos(pi/n) AREA : A = 1/4*n*s^2*cot(pi/n) or A = 1/2*n*R^2*sin(2*pi/n)

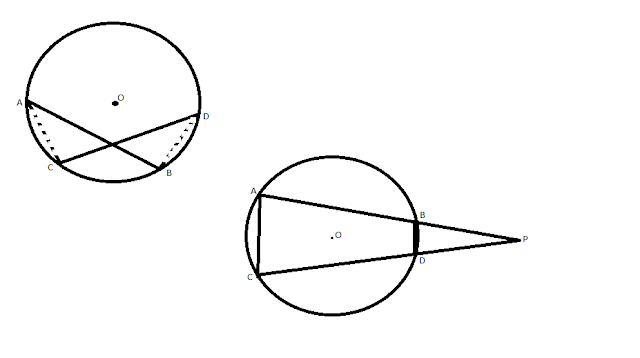
SOME RESULTS ON CIRCLES THEOREM 1. IF TWO ARCS OF A CIRCLE ARE CONGRUENT THEN THE CORRESPONDING CHORDS ARE EQUAL. THEOREM 2. THE PERPENDICULAR FROM THE CENTRE OF A CIRCLE TO A CHORD BISECT THE CHORD. THEOREM 3.  THE LINE JOINING THE CENTRE TO THE MID POINT OF A CHORD IS PERPENDICULAR TO THE CHORD. THEOREM 4.  THE PERPENDICULAR BISECTORS OF THE CHORDS OF A CIRCLE INTERSECT AT ITS CENTRE. THEOREM 5.  THERE IS ONE AND ONLY ONE CIRCLE PASSING THROUGH THREE NON COLLINEAR POINTS. (I) AN INFINITE NUMBER OF CIRCLE CAN BE DRAWN TO PASS THROUGH A SINGLE POINT. (II) AN INFINITE NUMBER OF CIRCLE CAN BE DRAWN TO PASS THROUGH TWO GIVEN POINTS. (III) A UNIQUE CIRCLE CAN BE DRAWN TO PASS THROUGH THREE GIVEN NON COLLINEAR POINTS. THEOREM 6.  EQUAL CHORDS OF CONGRUENT CIRCLES ARE EQUIDISTANT FROM THE CORRESPONDING CENTRES ARE EQUAL. THEOREM 7. CHORDS WHICH ARE EQUIDISTANT FROM THE CORRESPONDING CENTRES ARE EQUAL. THEOREM 8.  EQUAL CHORDS OF A CIRCLE ARE EQUIDISTANT F

FATHER OF ALGEBRA IMPORTANT FORMULAE OF ALGEBRA 1. (a+b)^2 = a^2 + b^2 + 2ab 2. (a-b)^2 = a^2 + b^2 - 2ab 3. (a+b)^2 = (a-b)^2 + 4ab 4. (a-b)^2 = (a+b)^2 - 4ab 5. a^2 - b^2 = (a-b)(a+b) 6. a^3 + b^3 = (a+b)(a^2 + b^2 - 2ab) 7. a^3 - b^3 = (a-b)(a^2 + b^2 + 2ab) 8. (a+b)^3 = a^3 + b^3 + 3ab(a+b) 9. (a-b)^3 = a^3 - b^3 - 3ab(a-b) 10. a^3 + b^3 = (a+b)^3 - 3ab(a+b) 11. a^3 - b^3 = (a-b)^3 + 3ab(a-b) 12. a^3 + b^3 + c^3 - 3abc = (a+b+c)(a^2 + b^2 + c^2 - ab - bc - ac)                                         OR       a^3 + b^3 + c^3 - 3abc = (a+b+c)1/2{2(a^2) + 2(b^2) + 2(c^2) - 2ab -2bc -2ac}                                         OR       a^3 + b^3 + c^3 - 3abc = 1/2(a+b+c)[(a-b)^2 + (b-c)^2 + (c-a)^2] 13. IF a+b+c = 0, THEN a^3 + b^3 + c^3 = 3abc 14. (a+b+c)^3 = a^3 + b^3 + c^3 + 3(b+c)(c+a)(a+b) 15. a^2 + b^2 = (a+b)^2 - 2ab 16. a^2 + b^2 = (a-b)^2 + 2ab 17. (a+b+c)^2 = a^2 + b^2 + c^2 + 2ab +2bc +2ca 18.  a^4 + b^4 +(a^2

SQUARE 1. PERIMETER = 4 * side = 4 * a  WHERE a = SIDE OF SQUARE 2. AREA = (side)^2 3. DIAGONAL = side * sqrt(2) 4. AREA OF THE PATH WHICH IS OUTSIDE OF SQUARE = 4 * (a + x) 5. AREA OF THE PATH WHICH IS INSIDE OF SQUARE = 4 * (a - x) WHERE x = WIDTH OF THE PATH TRAPEZIUM IT IS A QUADRILATERAL WHOSE OPPOSITE SIDES ARE PARALLEL. OTHER TWO OPPOSITE SIDES ARE OBLIQUE. 1. AREA = 1/2 * HEIGHT * (SUM OF PARALLEL SIDES)   HEIGHT IS THE DISTANCE BETWEEN THE TWO PARALLEL SIDES 2. MEDIAN = 1/2 * (SUM OF PARALLEL SIDES) MEDIAN IS THE SEGMENT JOINING THE MIDPOINTS OF OBLIQUE SIDES RHOMBUS IT IS PARALLELOGRAM WHOSE ALL SIDES ARE EQUAL.  ITS DIAGONALS BISECT EACH OTHER AT RIGHT ANGLE. 1. AREA = 1/2 * PRODUCT OF DIAGONALS 2. SIDE = sqrt {(D1/2)^2 + (D2/2)^2} 3. PERIMETER = 4 * SIDE WHERE D1 AND D2 ARE DIAGONALS

TRIANGLE 1. AREA = 1/2*BASE*HEIGHT   OR, √[s(s-a)(s-b)(s-c)] WHERE a, b, c  ARE THE LENGTHS OF THE SIDES OF TRIANGLE AND  s=(s+b+c)/2 2. AREA OF AN EQUILATERAL TRIANGLE =  √3/4 * (side)^2 3. AREA OF AN ISOSCELES TRIANGLE = b/4  √4(a^2)-(b^2) 4. PERIMETER OF AN EQUILATERAL TRIANGLE = 3 * SIDE RECTANGLE 1. AREA = LENGTH * BREADTH 2. PERIMETER = 2 (LENGTH + BREADTH) 3. DIAGONAL =  √(LENGTH)^2 + (BREADTH)^2 4. AREA OF PATH (OUTSIDE THE RECTANGLE) = 2 * (LENGTH + BREADTH + 2x) WHERE x= WIDTH OF THE PATH 5. AREA OF THE PATH INSIDE OF THE RECTANGLE = 2 * (LENGTH + BREADTH -2x) WHERE x= WIDTH OF THE PATH

IF SAME NUMBER IS THERE IN A SERIES LIKE 88888 OR 9999 UP TO AS MUCH AS YOU CAN.... IF YOU WANT TO FIND THEIR SUM LETS TAKE AN EXAMPLE 8888+888+88+8=? WE START FROM THE LEFT MULTIPLY 8 BY 1, 2, 3 & 4. U WILL GET YOUR ANSWER THOSE NUMBER WHOSE ALL DIGITS ARE 9 (99)^2=9801 (999)^2=998001 (9999)^2=99980001 (99999)^2=9999800001 THOSE NUMBER WHOSE ALL DIGITS ARE 3 (33)^2=1089                   THOSE NUMBER IN WHICH ALL DIGITS ARE NUMBER IS 3 TWO OR MORE THAN 2 TIMES REPEATED, TO FIND THE SQUARE OF THESE NUMBER,WE REPEAT 1 AND 8 BY (n-1). WHERE n= NUMBER OF TIMES 3 IS REPEATED (333)^2=110889 (3333)^2=11108889 TO CHECK 401 IS A PRIME NUMBER APPROXIMATE SQUARE ROOT = 20 PRIME NO < 20 ARE 2, 3, 5, 7, 11, 13, 17, 19 401 IS NOT DIVISIBLE BY ANY OF THESE PRIME NUMBERS SO 401 IS A PRIME NUMBER.

175 X 157 = ? THE RESULT OF MULTIPLICATION OF THREE DIGIT NUMBER IS 175 X 157 = 27475 STEP 1:  MULTIPLY  (5 X 7) = 35 (NOTE DOWN 5 CARRY 3) STEP 2: THEN DO CROSS MULTIPLICATION (7 X 7 + 5 X 5 + 3 (ADD CARRY)) = 77 (NOTE DOWN 7 CARRY 7) STEP 3: AGAIN (1 X 7 + 1 X 5 + 7 X 5 + 7 (ADD CARRY)) = 54 (NOTE DOWN 4 CARRY 5) STEP 4: DO CROSS MULTIPLICATION AND ADD CARRY  (1 X 5 + 1 X 7 + 5 (ADD CARRY)) = 17 (NOTE DOWN 7 CARRY 1) STEP 5: AGAIN (1 X 1 + 1) = 2, NOTE IT DOWN. AND FINALLY THE RESULT WE GET 27475

LET ME XPLAIN THIS RULE BY TAKING SOME EXAMPLES.... CONSIDER NUMBER 44679387, WE HAVE TO CALCULATE THE REMINDER ON DIVIDING THIS NUMBER BY 7 11 AND 13 RESPECTIVELY... MAKE TRIPLETS AS WRITTEN BELOW STARTING FROM UNITS PLACE 44.........679.........387 NOW ALTERNATE SUM = 44+387 = 431 AND 679 AND DIFFERENCE OF THESE SUMS = 679-431= 248 DIVIDE IT BY 7 WE GET REMINDER AS 3 DIVIDE IT BY 11 WE GET REMINDER AS 6 DIVIDE IT BY 13 WE GET REMINDER AS 1

LET'S LEARN HOW TO FIND SQUARE ROOT BY TAKING DIFFERENT EXAMPLES.... EXAMPLE: FIND THE SQUARE ROOT OF 4489 WE GROUP THE LAST PAIR OF DIGITS, AND THE REST OF THE DIGITS TOGETHER. NOW, SINCE THE UNIT DIGIT OF 4489 IS 9. SO WE CAN SAY THAT UNIT DIGIT OF ITS SQUARE ROOT WILL BE EITHER 3 OR 7. NOW CONSIDER FIRST TWO DIGITS i.e. 44. SINCE 44 COMES BETWEEN THE SQUARES OF 6 ND 7 (i.e. 6^2 < 44< 7^2),SO WE CAN DEFINITELY SAY THAT THE TEN'S DIGIT OF THE SQUARE ROOT OF 4489 WILL BE 6. SO, FAR WE CAN SAY THAT THE SQUARE ROOT WILL BE EITHER 63 OR 67. NOW WE WILL FIND THE EXACT UNIT DIGIT. TO FIND THE EXACT UNIT DIGIT, WE CONSIDER THE TEN'S DIGIT i.e, 6 ND THE NEXT TERM i.e, 7. MULTIPLY THESE TWO TERMS SINCE, 44 IS GREATER THAN 42. SO SQUARE ROOT OF 4489 WILL BE THE BIGGER OF THE TWO OPTIONS i.e, 67.

LETS DISCUSS SOME BASIS IDEAS IN MATHEMATICS WHETHER YOU LOVE MATHS, OR DESPITE IT, THE FOLLOWING TRICKS CAN TURN YOU INTO A MATH WHIZ-OR AT LEAST WILL HELP TO SPEED UP SOME OF THE CALCULATIONS YOU NEED TO DO IN YOUR HEAD. I'VE INCLUDED FIVE OF MY FAVORITES HERE........ QUICK SQUARE IF YOU NEED TO SQUARE A 2 DIGIT NUMBER ENDING IN 5, MULTIPLY THE FIRST DIGIT BY ITSELF PLUS 1, AND PUT 25 ON THE END. THAT'S ALL! (25)^2=(2*(2+1))&25 2*3=6 & 25 625 MULTIPLYING BY 9 TO MULTIPLY ANY NUMBER BETWEEN 1 AND 9 BY 9, HOLD BOTH HANDS IN FRONT OF UR FACE, WITH FINGERS EXTENDED. NOW DROP THE FINGER THAT CORRESPONDS TO THE NUMBER YOU R MULTIPLYING (FOR EXAMPLE, FOR 9*3, DROP UR THIRD FINGER). NOW COUNT THE FINGERS BEFORE THE DROPPED FINGER(IN THE CASE OF 9*3 IT IS 2)-THAT'S UR FIRST DIGIT. THEN, COUNT THE FINGERS AFTER (AGAIN IN THE CASE, IT'S 7). THE ANSWER IS 27. DIVIDING BY 5 TO DIVIDE A LARGE NUMBER BY 5, ALL YOU NEED TO DO IS MULTIPLE

LE TS TAKE AN EXAMPLE OF ANY 2 DIGIT NUMBER Let us take 57 so, (57)^2 first of all square the unit place number i.e, 7 and its square is 49 Then square tens place number i.e, 5 and its square is 25 and then take 5 and 7 and multiply them 7*5=3 and  also multiply 35 by 2 i.e,35*2=70 now write in this format  25  70  49 now take 4 of 49 and add it to the left of 49 i.e, 70 but you have add in 0 i.e, 0+4=4 and now take 7 of 70 and add it to 25 i.e, 25+7=32 so,  the square is 3249.